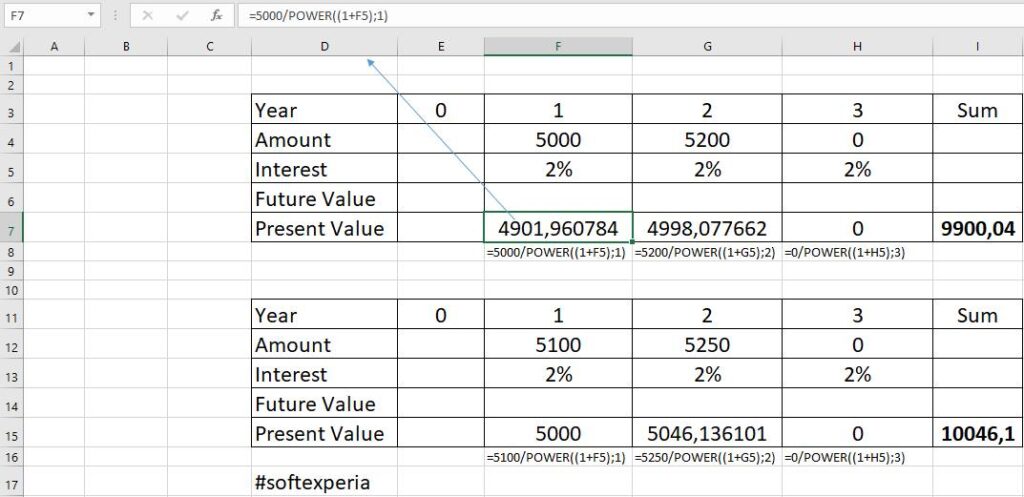
Μελλοντική αξία (FV) ενός σημερινού ποσού Παρούσα αξία (PV) ενός μελλοντικού ποσού Παράδειγμα Μελλοντικής Αξίας (Future Value – FV) Σενάριο: Έχεις σήμερα 5.000 € και τα καταθέτεις σε μια τράπεζα με ετήσιο επιτόκιο 4%, για 5 χρόνια, με ετήσιο ανατοκισμό. Θέλεις να βρεις: Πόσα θα έχεις στο τέλος των 5 ετών; Βήμα 1: Γράφουμε τα δεδομένα Παρούσα αξία (PV) = 5.000 € Επιτόκιο (r) = 4% = 0,04 Περίοδοι (n) = 5 έτη Ζητούμενο: Μελλοντική αξία (FV) Βήμα 2: Τύπος μελλοντικής αξίας Βήμα 3: Αντικαθιστούμε τα δεδομένα Βήμα 4: Ερμηνεία Αν επενδύσεις 5.000 € σήμερα με επιτόκιο 4% για 5 χρόνια, στο τέλος θα έχεις περίπου 6.083,26 €. Η διαφορά 6.083,26 – 5.000 = 1.083,26 € είναι οι τόκοι που κέρδισες συνολικά (και περιλαμβάνουν και τον ανατοκισμό). Παράδειγμα Παρούσας Αξίας (Present Value – PV) Σενάριο: Σου υπόσχονται ότι θα λάβεις 10.000 € σε 3 χρόνια. Το κατάλληλο προεξοφλητικό επιτόκιο (δηλαδή…
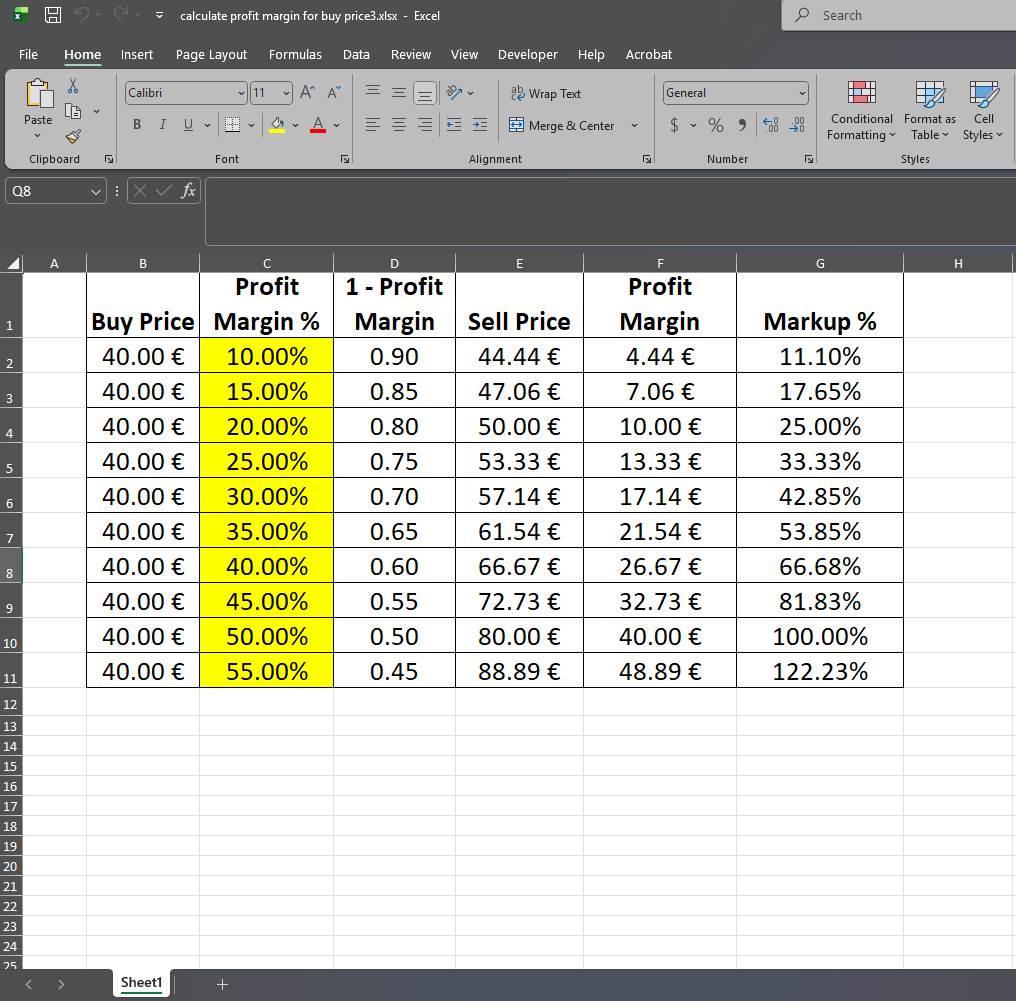
✅ Understanding Profit Margin, Markup, and Selling Price (With Example Table) When you run a business, knowing how to correctly price your products is essential. Two of the most common pricing metrics are profit margin and markup. Although people often mix them up, they are not the same thing. Let’s break it down using the example above, where every product has a €40.00 buy cost. ✅ 1. Profit Margin % Profit margin shows how much profit you earn as a percentage of the selling price. Example: Buy Price: €40.00 Profit Margin: 25% Sell Price becomes €53.33 Profit earned: €13.33 Formula: Sell Price = Buy Price / (1 − Profit Margin) ✅ 2. Sell Price This is the final price you charge the customer after applying the profit margin. You can see how the selling price increases as the margin goes up. Example: 10% margin → €44.44 selling price 40% margin…
24 ACCOUNTING BASICS THAT EVERYBODY NEEDS TO KNOW 1. ASSETS Resources owned by a business that have economic value. 2. LIABILITIES Obligations or debts owed by a business. 3. EQUITY The owner’s interest in the business. 4. REVENUE Income earned from normal business operations. 5. EXPENSES Costs incurred in the process of earning revenue. 6. PROFIT Financial gain after deducting expenses from revenue. 7. LOSS Occurs when expenses exceed revenue. 8. CASH FLOW The movement of money in and out of a business. 9. GROSS MARGIN Revenue minus the cost of goods sold. 10. NET INCOME Total revenue minus total expenses. 11. BALANCE SHEET Financial statement showing assets, liabilities, and equity. 12. INCOME STATEMENT Financial statement showing revenue, expenses, and profit over time. 13. CASHFLOW STATEMENTS Financial statement showing cash inflows and outflows. 14. DEBITS AND CREDITS Entries used to record transactions in double-entry accounting. 15. JOURNAL ENTRIES Records of…
Business Ownership, Base Rates, Debt & Credit Ratings 1. Business Ownership – Importance Business ownership affects control, liability, taxes, profit sharing, ability to grow, and access to finance. 2. Types of Business Ownership A. Sole Trader – Owned by one person, simple to set up, full control. – Unlimited liability, harder to raise finance. B. Partnership – 2–20 owners, shared workload and skills. – Profit sharing, potential disputes, liability depends on type. C. Limited Company (Ltd) – Separate legal identity, limited liability, can raise more funds. – More regulation and administration. D. Public Limited Company (PLC) – Shares can be publicly traded, raises large finance. – High regulation, shareholder pressure. 3. Base Rate – Interest rate set by central banks. – High base rate: borrowing expensive, inflation falls. – Low base rate: borrowing cheap, economy grows. 4. Debt – Borrowed money to be repaid with interest. Personal debts: student loans,…
Χρηματοοικονομικά μαθηματικά – Ράντες Ράντα καλούμε ένα σύνολο χρηματικών ποσών που καταβάλλονται, δηλαδή γίνεται κατάθεση ή ανάληψη αυτών, ανά ίσα χρονικά διαστήματα. Ο όρος ράντα έχει προέλθει από το Λατινικό όρο Reddita. Στην αγγλική γλώσσα, ο αντίστοιχος όρος είναι Rent ή Annuity. Ένας ελληνικός όρος που θα μπορούσε να αποδώσει καλύτερα την έννοια αυτή είναι χρηματοσειρά ή χρηματοροή, διότι όπως θα δούμε στη συνέχεια οι ράντες αποτελούνται πράγματι από σειρές χρηματικών καταθέσεων ή πληρωμών. Τα προβλήματα που αναφέρονται σε ράντες είναι συνήθως δημιουργία κεφαλαίου με ανατοκισμό καταθέσεων σε ίσα χρονικά διαστήματα ή εξόφληση ενός χρέους (δανείου κ.λ.π.) με δόσεις που καταβάλλονται επίσης σε ίσα χρονικά διαστήματα. Παραδείγματα ραντών από την καθημερινή ζωή του ανθρώπου είναι το ενοίκιο που καταβάλλει κάποιος, οι μηνιαίες κρατήσεις στο μισθό των εργαζομένων για τα διάφορα ασφαλιστικά ταμεία, οι ετήσιες ή εξαμηνιαίες ή μηνιαίες δόσεις για την εξόφληση δανείων κ.λ.π. Όρος ράντας καλείται το χρηματικό ποσό…
Θέλεις να αγοράσεις ένα αυτοκίνητο που κάνει 15100 ευρώ και μπορείς να δίνεις 325 ευρώ το μήνα. Computing Amount to Borrow and Down Payment Αν το επιτόκιο είναι 7,5% (μηνιαίος εκτοκισμός) και οι μηνιαίες δόσεις 48, πόσα μπορείς να δανειστείς; Πόσα πρέπει να δώσεις μπροστά; Απάντηση : Πρέπει να δώσεις 1651,61 ευρώ μπροστά και να δανειστείς 13448,39 ευρώ (παρούσα αξία). #softexperia
Στη σελίδα μας στο facebook: Σύνδεσμος Εμπορ Αντιπροσώπων & Διαν Δυτικής Ελλάδας, Πελοπον., Ηπείρου, ΙΝ, μπορείτε να βρείτε άρθρα σχετικά με την επικοινωνία, τη διαπραγμάτευση, τις πωλήσεις, τα προβλήματα των αντιπροσώπων και των διανομέων και την οικονομία. Μη διστάσετε να επικοινωνήσετε μαζί μας στο email : info@seade.gr για να συζητήσουμε περισσότερο τα προβλήματα του κλάδου αλλά και τυχόν εξειδικευμένα ζητήματα που σας απασχολούν. Επικοινωνία : 6931 131417, 6944 522119 -> https://bit.ly/3FF11GE
Προεξόφληση Οι επιχειρήσεις πολλές φορές προσφέρουν προϊόντα ή και υπηρεσίες στους πελάτες τους με πίστωση, δηλαδή τους δίνουν τη δυνατότητα να εξοφλήσουν το ποσό της αξίας του αγαθού που αγόρασαν σε κάποιο καθορισμένο χρονικό διάστημα στο μέλλον. Για να εξασφαλίσουν την καταβολή των χρημάτων τους από τους πελάτες τους, τους καλούν να υπογράψουν έναν πιστωτικό τίτλο ο οποίος ονομάζεται αξιόγραφο (γραμμάτιο ή συναλλαγματική ή επιταγή). Με τον τρόπο αυτό διασφαλίζεται η εξόφληση του χρέους προς τις επιχειρήσεις στην αναγραφόμενη στο αξιόγραφο ημερομηνία. Για λόγους ρευστότητας, οι επιχειρήσεις πολλές φορές μεταβιβάζουν την είσπραξη αξιογράφων τους σε πιστωτικά ιδρύματα και πληρώνουν κάποιο χρηματικό ποσό για τη μετατροπή σε χρήμα των αξιογράφων πριν από τη λήξη τους. Η ρευστοποίηση αυτή καλείται προεξόφληση. Προεξόφλημα καλείται το χρηματικό ποσό, ο τόκος, που κρατάνε τα πιστωτικά ιδρύματα κατά την προεξόφληση των αξιογράφων. Στην Ελλάδα, όσο και στην υπόλοιπη Ευρώπη, πλην της Αγγλίας, το προεξόφλημα υπολογίζεται με…
Here’s a simple HTML dashboard that calculates the monthly payment, total cost of the house, and displays an amortization schedule along with a chart. This example uses JavaScript for calculations and Chart.js for the chart visualization. Mortgage Dashboard House Price: $1,450,000 Downpayment: $625,000 Loan Amount: $825,000 Interest Rate: 3.75% Loan Term: 25 years Click Mortgage Dashboard to view it. # Explanation: 1. Calculations: – The monthly payment is calculated using the formula for an amortizing loan. – The total cost of the house includes the down payment and total payments over the loan term. 2. Amortization Schedule: – The schedule is generated for each year, showing the beginning balance, ending balance, principal paid, interest paid, and cumulative totals. 3. Chart: – A line chart visualizes the cumulative principal and interest paid over the years using Chart.js.
Η παρούσα αξία είναι το ποσό χρημάτων που έχεις τώρα, ενώ η μέλλουσα αξία είναι το ποσό που θα έχεις στο μέλλον αν επενδύσεις ή αποταμιεύσεις τα χρήματά σου. Φαντάσου ότι έχεις 10 ευρώ σήμερα. Αν τα βάλεις σε μια τράπεζα που σου δίνει τόκο, μετά από ένα χρόνο μπορεί να γίνουν 11 ευρώ. Τα 10 ευρώ είναι η παρούσα αξία και τα 11 ευρώ είναι η μέλλουσα αξία. Παράδειγμα: Αν σήμερα έχεις 10 ευρώ και αποφασίσεις να τα αποταμιεύσεις για ένα χρόνο με 10% τόκο, στο τέλος του χρόνου θα έχεις 11 ευρώ. Έτσι, τα 10 ευρώ είναι η παρούσα αξία και τα 11 ευρώ είναι η μέλλουσα αξία.
Η παρούσα αξία (PV) είναι η αξία ενός ποσού χρημάτων που θα λάβουμε στο μέλλον, προσαρμοσμένη με βάση ένα συγκεκριμένο επιτόκιο. Αντίθετα, η μέλλουσα αξία (FV) είναι η αξία ενός ποσού χρημάτων σήμερα, αν επενδυθεί για μια συγκεκριμένη περίοδο με ένα συγκεκριμένο επιτόκιο. # Παράδειγμα: Ας πούμε ότι θέλουμε να υπολογίσουμε την παρούσα αξία 1.000 ευρώ που θα λάβουμε σε 5 χρόνια, με επιτόκιο 5%. Μέλλουσα αξία (FV): FV = PV × (1 + r)^n FV = 1.000 × (1 + 0,05)^5 = 1.000 × 1,27628 ≈ 1.276,28 ευρώ Παρούσα αξία (PV): PV = FV / (1 + r)^n PV = 1.000 / (1 + 0,05)^5 = 1.000 / 1,27628 ≈ 783,53 ευρώ # Πότε συμφέρει να επενδύσουμε: Αν έχουμε 783,53 ευρώ σήμερα και τα επενδύσουμε με επιτόκιο 5% για 5 χρόνια, θα έχουμε 1.000 ευρώ στο τέλος της περιόδου. Αν η επένδυση μας αποφέρει περισσότερα από 783,53 ευρώ σε…
Ο Κανόνας του 72 Διαιρέστε απλώς το 72 με το επιτόκιο. Μια επένδυση με ετήσια απόδοση 9% θα διπλασιαστεί περίπου σε 8 έτη (72:9). Μπορείτε να επιτύχετε μεγαλύτερη ακρίβεια χρησιμοποιώντας τον αριθμό 69 ή 70, αλλά το 72 είναι συνήθως πιο βολικό επειδή έχει περισσότερους διαιρέτες. Παραδείγματα Αν θέλετε να ξέρετε πόσο καιρό θα σας πάρει να διπλασιάσετε τα χρήματά σας με 8% επιτόκιο, διαιρείτε 72 δια του 8 και παίρνετε 9 χρόνια. Ο κανόνας του 72 είναι ακριβής, αρκεί το επιτόκιο να είναι λιγότερο από είκοσι τοις εκατό. Μπορείτε να κάνετε και το ανάποδο. Αν θέλετε να διπλασιάσετε τα χρήματά σας σε έξι χρόνια, απλώς διαιρέστε το 72 δια του 6, για να βρείτε ότι θα χρειαστεί ένα επιτόκιο γύρω στα 12%. Δείτε το σχετικό βίντεο στο YouTube : https://www.youtube.com/watch?v=jc_IAFQAk6M Διαβάστε περισσότερα στο βιβλίο του Morton Davis. “Τα μαθηματικά του χρήματος” #softexperia #ο_κανόνας_του_72
Τι σημαίνει αγορά χρέους; Όταν κάποιος αγοράζει χρέος, δεν βρίσκεται να χρωστά περισσότερα. Το αντίθετο. Αποκτά το δικαίωμα είσπραξης των χρημάτων που οφείλονταν προηγουμένως σε κάποιον τρίτο οργανισμό, φορέα ή πωλητή. Τα χρέη που οφείλονται από ιδιώτες, επαγγελματίες και ιδιώτες σε τράπεζες, χρηματοπιστωτικούς οργανισμούς, εταιρείες κοινής ωφέλειας, εταιρείες παροχής ιατρικών υπηρεσιών και άλλες επιχειρήσεις μπορούν να γίνουν αντικείμενο αγοραπωλησίας. Το ποσό μιας τέτοιας αγοραπωλησίας παρουσιάζει μεγάλες διακυμάνσεις. Όσο μικρότερη είναι η πιθανότητα είσπραξης του χρέους, τόσο μικρότερη η τιμή του, π.χ. 20 λεπτά για κάθε 1 ευρώ αγοράς χρέους. Κάθε μέρα ακούμε ότι ακόμα ένα χαρτοφυλάκιο κανονικών ή κόκκινων δανείων πουλήθηκε σε ένα fund. Ανεξάρτητα από το ποσό αγοράς χρέους, ο αγοραστής διατηρεί το δικαίωμα απαίτησης στο 100% του ποσού της αγοράς χρέους. Αν π.χ. έδωσε 100 ή 200 ευρώ για αγορά 1000 ευρώ χρέους, τότε ο αγοραστής διατηρεί το δικαίωμα να εισπράξει 1000 ευρώ. Είναι στην διακριτική του ευχέρεια…
Assymetry of returns – Ασυμμετρία αποδόσεων Από οποιοδήποτε σημείο αναφοράς, το να κερδίζεις 50% και το να χάνεις 50% δεν σε αφήνει στο ίδιο σημείο. 1000 + 50% κέρδος = 1500 1500 – 50% ζημιά = 750 Την επόμενη φορά που θα σας πουν ότι υπάρχει βελτίωση μεγεθών προς τα πάνω ή προς τα τα κάτω, καλό είναι να ρωτάτε και το σημείο αναφοράς.
Απόσβεση πάγιων στοιχείων ενεργητικού μιας επιχείρησης Για την απόκτηση ενός μηχανήματος μια επιχείρηση πλήρωσε αρχικό κόστος A 5000 ευρώ και η υπολειμματική του αξία S, μετά από 10 έτη έγινε 600 ευρώ. Να υπολογιστεί το ετήσιο ποσό για την απόσβεση του μηχανήματος, αν ξέρουμε ότι το ετήσιο επιτόκιο απόσβεσης είναι 5,75%. Α = 5000 € S = 600 € n = 10 έτη, i = 5,75% ή 0,0575 Η αξία προς απόσβεση του μηχανήματος είναι 5000 – 600 = 4400 €. Άρα R = 4400 * 0,0767633 = 337,76 € Δηλαδή η ετήσια δαπάνη R της επιχείρησης για την απόσβεση του μηχανήματος είναι 337,76 €. * Στη φωτοφραφία η σχέση για τον υπολογισμό του ποσού R της ετήσιας απόσβεσης του μηχανήματος.
Κεφάλαιο 100€ ανατοκίζεται με ετήσιο επιτόκιο 3% για 4 έτη και 5 μήνες. Να βρεθεί η τελική αξία αυτού. Δεδομένα Αρχικό κεφάλαιο K = 100 ευρώ n = years, χρόνια m = months, μήνες i = interest, επιτόκιο Απάντηση Η τελική αξία είναι 113,95€. #maths #softexperia #ανατοκισμός #υπολογισμός_αξίας #γραμμική_συνθήκη
Want to forecast future sales using your own code? Learn how to build a simple yet powerful PHP function that predicts future values based on historical sales data — just like Excel’s FORECAST.LINEAR! No external libraries needed. Want to predict your own sales in PHP?Get the complete code, step-by-step guide, and learn how to make your own forecast Need help with something more advanced, like multi-variable forecasting or integration with your database?Contact me — I can help you build it! This is the PHP code you can register in your theme’s functions.php file and this is the shortcode you should add to your post : // Forecast sales function forecast_sales_shortcode($atts) { // Default attributes (you can override in the shortcode) $atts = shortcode_atts([ ‘months’ => ‘1,2,3,4,5,6,7’, ‘sales’ => ‘18500,20000,18000,22000,23000,23500,23800’, ‘forecast’ => ‘8,9,10’ ], $atts); $months = array_map(‘intval’, explode(‘,’, $atts[‘months’])); $sales = array_map(‘floatval’, explode(‘,’, $atts[‘sales’])); $futureMonths = array_map(‘intval’, explode(‘,’, $atts[‘forecast’])); //…
Ας υποθέσουμε ότι μια εμπορική επιχείρηση αγοράζει από έναν προμηθευτή με τριμηνιαίες διορίες (δηλ. έχει 90 ημέρες μέχρι να πληρώσει τον λογαριασμό του προμηθευτή) και πουλά στους πελάτες της σε 30 ημέρες. Η εταιρεία αυτή μπορεί να χρησιμοποιήσει τις εισπράξεις για Χ διάστημα αγορασμένου αποθέματος προτού να χρειαστεί να πληρώσει τον προμηθευτή της. Κάνει χρήση άτοκου κεφαλαίου κίνησης πουλώντας στον πελάτη με αντάλλαγμα πιο σύντομο χρόνο πληρωμ΄ής π.χ. 30 ημέρες και πληρώνοντας τους προμηθευτές έπειτα από 60 ή 90 ή 120 ή μπορεί και 150 ημέρες. Γι’ αυτό και πολλοί έμποροι χονδρικής ή λιανικής πώλησης με “γεμάτο” ταμείο προσφέρουν και άλλες οικονομικές υπηρεσίες. Παράγουν πολλά μετρητά, χωρίς ανάγκη αύξησης κεφαλαίου κίνησης, τα οποία μπορούν να χρησιμοποιήσουν, προτού να χρειαστεί να πληρώσουν τους προμηθευτές τους. Παράδειγμα Στο παρακάτω παράδειγμα μια εμπορική επιχείρηση πουλάει στους πελάτες τους με πληρωμή σε 30 ημέρες και πληρώνει τους προμηθευτές τους σε 90 ημέρες. Με κόστος…